la relativité restreinte : La dilatation du temps

Je vais me servir de cette transformation de Lorentz pour expliquer les phénomènes de dilatation du temps et de contraction des longueurs. Mais avant cela je vais vous donner deux exemples les illustrant.

         Imaginons que des jumeaux aient exactement le même âge sur Terre, l’un d’eux reste sur le plancher des vaches tandis que l’autre part dans une fusée à une vitesse proche de la lumière ; il aurait dû revenir sur Terre un an après son départ mais il ne revint pas. Deux ans après il n’était toujours pas de retour. Il arriva enfin 25 ans après son départ de la Terre. Pour lui le voyage n’avait duré qu’un an mais qu’elle ne fut pas sa surprise de voir que son frère jumeau avait, comme tous les autres habitants de la Terre, vieilli de 25 ans. Ils n’étaient donc plus vraiment des jumeaux. Ce phénomène est dû à la dilatation du temps. Le temps ne s’écoule pas de la même façon (il est beaucoup plus lent) pour un référentiel qui va à une vitesse proche de celle de la lumière.

Il y a moyen de mettre en évidence théoriquement l’âge que devrait avoir le cosmonaute et son frère jumeau. En effet, imaginons que le cosmonaute parte dans sa fusée à destination d’une planète se situant à 10 années lumières. Il lui faudrait donc 10 ans pour aller sur cette planète à la vitesse de la lumière ( notée c ). La fusée utilisée par celui-ci irait, par exemple, à une vitesse égale à 270000 km/s , c’est-à-dire à une vitesse égale aux neuf dixièmes de la vitesse de la lumière.

La durée du voyage par rapport au référentiel du voyageur peut être calculée.

 En effet, nous savons que la fusée va devoir parcourir une distance L qui est égale à :

L= c. 10ans

(l’espace est égal à la vitesse multipliée par le temps pour un objet se déplaçant à une vitesse constante)

 Mais la vitesse de la fusée est de 9/10 de   c , le temps pour parcourir la distance est donc plus long, notons le   t . Nous pouvons le calculer de la façon suivante :

L= c . 10 ans = v . t

Donc, t = c/v . 10 ans = 11,1111 ans car c/v = 10/9

Pour faire le voyage aller-retour le cosmonaute mettra donc 22,2222 ans.

Si le jumeau, resté sur Terre, avait 18 ans au départ de la fusée, il aura donc 40,2222 ans au retour de son frère. Si le temps s’écoule de la même manière pour tout le monde alors le cosmonaute devrait avoir le même âge que son frère. Mais le temps ne s’écoule pas comme cela, il se dilate. Nous pouvons dire que l’âge qu’aura le cosmonaute à son retour sera de 33,3333 ans. 

Mais pour montrer cela nous allons avoir besoin de la théorie de la relativité. Ce qui sera montré une fois que nous l’aurons découverte au cours de ce TFE. 

        Bien sûre ceci n’était qu’une histoire fantastique. Mais des expériences ont déjà eu lieu sur Terre et parmi celles-ci il y en a une qui démontre que le temps se dilate. Actuellement les horloges les plus précises sont les horloges atomiques. Deux de celles-ci avaient été mise à la même heure avec une très grande rigueur. La première est restée sur Terre, l’autre a été installée dans un avion qui vola à grande vitesse et parcouru une certaine distance. A son retour, celle qui se trouvait dans l’avion était légèrement « décalée » par rapport à celle qui était restée sur terre. Elle avait un millionième de seconde en moins. La différence est donc infime, mais elle est malgré tout observable au moyen d’horloges d’une telle précision.

         Le titre de ce chapitre porte le nom de dilatation ; il me faut donc vous expliquer pourquoi nous ne parlons que de dilatation et non de contraction. Reprenons l’exemple de la fusée. Quel que soit le référentiel que nous choisirons (pour cet exemple, les deux référentiels possibles sont la Terre et la fusée), nous aurons toujours l’impression que c’est, dans le référentiel de la Terre, le cosmonaute qui se déplace à une vitesse proche de la lumière par rapport à son frère tandis que dans l’autre référentiel nous penserons que c’est le frère qui se déplace à une vitesse très importante par rapport au cosmonaute. Chacun des deux frères aura donc l’impression que l’autre vieillit plus vite que lui. Nous ne parlerons donc que de dilatation du temps.

Le fait que le cosmonaute soit plus jeune que son frère à son retour ne peut-être traité à partir de la relativité restreinte. En effet, celle-ci n’est valable que pour les corps qui sont en MRU  (cfr chapitre 2.1.). Or pour que la fusée atteigne sa vitesse de croisière, elle doit subir une accélération. Nous ne pouvons donc pas utiliser la restreinte pour expliquer que le cosmonaute sera moins vieux que son frère. 

        Maintenant utilisons la transformation de Lorentz pour montrer que l’hypothèse du temps absolu doit être abandonnée. Nous savons que

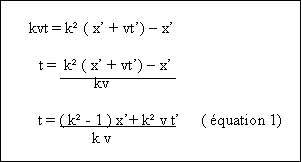
De plus nous savons que :   k = 1 / (1 – β²)^1/2    . Donc,   k² = 1/ ( 1 – β²) . Nous pouvons donc dire que

Nous pouvons donc remplacer   k²-1   dans l’équation 1, nous obtenons alors :

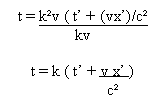
Nous pouvons aussi isoler   t’   comme nous venons de le faire pour   t  :

Nous constatons une réciprocité parfaite entre les deux équations. De plus si la vitesse de déplacement de b par rapport à a ( cfr chapitre 3.2b) est beaucoup plus petite que la vitesse de la lumière, c’est à dire qu’elle peut correspondre par exemple aux vitesses de la vie courante, à ce moment-là les temps   t   et   t’  sont égaux car   v/c   est proche de   0   et   k   est proche de   1 .

         Pour montrer la dilatation du temps à partir des formules il nous faut encore les développer, pour cela nous allons observer les conséquences des formules de Lorentz

 x’ = k (x - vt) et x = k ( x’ + vt’)

 ainsi que les formules que nous venons de découvrir : 

Prenons deux événements distincts, nous pouvons déterminer leurs coordonnées d’espace et de temps dans les deux systèmes   a   et   b .

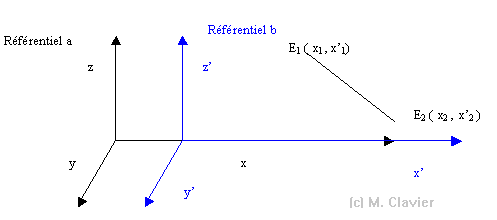
Les coordonnées de   E₁   et de   E₂   ( deux événements ayant lieu en même temps, comme, par exemple, deux lampes qui s’allument) sont les mêmes pour les axes   z, z’   et   y, y’ . Par contre elles sont différentes pour les axes   x   et   x’  ; elles vont se noter   x₁   et   x’₁   ainsi que   x₂ et   x’₂ . Or nous avons vu précédemment que  

x = k . (x’ + vt’)   et que   x’ = k . ( x – vt) . Nous pouvons donc utiliser ces deux formules pour les coordonnées des points que nous  sommes en train d’observer. En effet,   x₁ = k . (x’₁ + vt’₁)   et   x₂ = k . (x’₂ + vt’₂).

Or nous savons que la variation de   x , notée   Δx , est égale à   x₂ – x₁      ( loi mathématique de base) et que   Δx’ = x’₂ – x’₁  ; de même   Δt = t₂ – t₁   et

Δt’ = t’₂ – t’₁  . 

Cela implique que  Δx = k (Δx’ + v Δt’)   et que   Δx’ = k ( Δx – v Δt ) . Nous pouvons faire la même chose pour les résultats que nous avons obtenus à la page précédente :

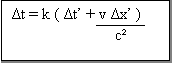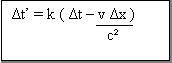Ces formules vont nous permettre de montrer que le temps n’est pas absolu, que celui-ci se dilate d’autant plus que la vitesse est grande. Pour montrer cela observons un événement commun aux deux référentiels a et b, c’est-à-dire, qu’ici,   E₁ = E₂  .   Δx’  est donc égal à   0   (  Δx’  est en fait la coordonnée sur l’axe   x   de l’événement   E₁    moins celle de l’événement   E₂  ). Puisqu’il y a toujours un déplacement du référentiel   a  par rapport à   b  (et inversement) et que les temps   Δt   et   Δt’   sont différents, nous pouvons donc en déduire, grâce aux formules ci-dessus, que   Δt = k Δt’   car   Δx’ = 0 .

  Or,    k = 1 /      (1 – β² )^1/2    nous pouvons donc dire que Δt est beaucoup plus grand que Δt’ sauf si v<<<c, ce qui impliquerait que k serait égal à 1. Cela signifie qu’au repos ou, du moins, quand la vitesse à laquelle se meuvent les deux référentiels est petite par rapport à la vitesse de la lumière, les temps sont égaux tandis que quand la vitesse est non négligeable les temps   Δt   et   Δt’   sont différents.

Par définition la dilatation du temps, c’est tout mécanisme physique qui définit une durée   Δt   (qui est égale à   Δt’  ) quand il se trouve au repos et définit une durée   Δt = k Δt’   quand il se meut à la vitesse   v   dans le référentiel   a  .

Par contre quand on considère que c’est le référentiel a qui se meut par rapport au référentiel   b , alors la formule appropriée est   Δt’ = k Δt .

Donnons un exemple concret pouvant être utilisé dans ce cas-ci.

Il existe des particules qui sont créées par interaction entre les rayons du soleil et la haute atmosphère ; elles s’appellent muons ou “mésons μ”. Celles-ci sont très instables et ont une durée de vie très courte. Cette durée fut mesurée en laboratoire en produisant des muons, elle est égale à 2,1 . 10^-6 s lorsqu’ils sont au repos.

Etant donné cette dernière, les muons ne pourraient donc pas parcourir une distance bien grande même si leur vitesse est proche de la lumière lorsque qu’ils sont “créés” dans notre atmosphère. En effet cette distance devrait être égale à   vt , c’est-à-dire à  2,1 . 10^-6  . 3 . 10⁸. Celle-ci est donc de 620 mètres. Or chose étrange, des muons arrivent au sol alors qu’ils ont été créés dans notre haute atmosphère, donc à une distance beaucoup plus grande. Nous pouvons comprendre ce phénomène avec les formules que nous avons obtenues précédemment; en effet la vitesse du muon est de 0,99995 fois celle de la lumière.   k   est donc égal à 100. Nous devons donc, pour un observateur terrestre, dilater le temps de vie du muon d’un facteur 100. Il parcourt donc 62 km et non 620 mètres.

Nous en revenons donc à nous poser une question: pourquoi est-ce que vu du muon la distance parcourue de la haute atmosphère jusqu’au sol est-elle égale à 620 mètres?

Pour y répondre il nous faut ouvrir un nouveau chapitre, celui de la contraction des longueurs.

(c) Michaël Clavier 2004 - document protégé par les droits d'auteur. toute reproduction doit obtenir l'accord écrit de son auteur.