Nucléaire - Loi de décroissance radioactive

Un noyau radioactif émet un rayonnement afin d'atteindre un état de plus grande stabilité. Toutefois, si l'on place un détecteur à proximité d'un noyau radioactif, l'on ne peut prédire l'instant où celui-ci va se désintégrer. Le processus de désintégration est un processus statistique. La radioactivité est un phénomène nucléaire indépendant des conditions physiques dans lequel se trouve l'élément et de son état chimique.

Malgré cela, si l'on prend un échantillon contenant de nombreux noyaux radioactifs N, nous pouvons mesurer l'activité de l'échantillon (source) notée A(t). Cette activité est le nombre de rayonnement émis par unité de temps.

Chaque fois qu'un rayonnement est émis, la quantité de noyaux radioactifs diminue de la même quantité. A chaque rayonnement émis, un noyau radioactif se transforme en un élément plus stable. Ce qui peut s'écrire :

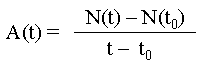  où N(t) est la population de noyaux radioactif après t secondes et N(t₀) la population au départ. Le moins provient du fait que la population radioactive diminue avec le temps.

Si l'échantillon est très grand, l'on peut considérer N(t) comme une fonction continue :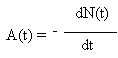

L'activité ne dépendant que de la nature du noyau et étant proportionnelle à la population (N), nous pouvons écrire :

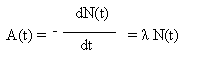avec λ étant une constante dépendant de la nature du noyau.

Il faut trouver une fonction dont la dérivée redonne la fonction au signe près. Cette fonction N(t) doit être égale à λ N(t).

N(t) = N₀ e^-λt   (fonction exponentielle) 

Cette équation vérifie l'égalité :

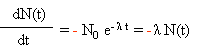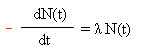=> , avec N₀ représentant la population (nombre de moles) au temps t = 0.

N(t = 0) = N₀ . e^-λ0 = N₀ , car e⁰ = 1

De même;

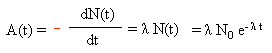
d'où :

où A₀ = l'activité initiale au temps t = 0 et égal à λ N₀ 

N = évolution du nombre initial de noyaux exprimée en moles au cours du temps.

A = l'activité de l'échantillon exprimée en désintégrations/s

λ = une constante propre à une même espèce de noyaux.

L'activité (A) et la population (N) décroissent donc toutes les deux en suivant une fonction exponentielle appelée loi de décroissance radioactive. Ci-dessous : l'évolution de la population au cours du temps.

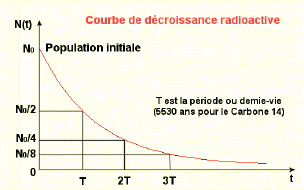T = la période ou temps de demi-vie. cette période est égale au temps nécessaire pour que la population N, ai diminué de moitié :.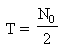

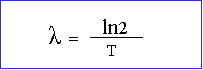
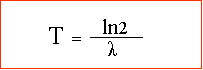
L'on peut donc en déduire que T, le temps de demi-vie dépend du type de noyaux.

... quelques chiffres :

Notez que des isotopes d'un même élément n'ont pas le même type de radioactivité ni les mêmes temps de demi-vie. Ce temps de demi-vie dépend donc bien de la nature du noyau.