 |
|
|
|
Si aucune force n'agit sur lui, la vitesse d'un corps mobile et la direction de son mouvement restent constantes selon la première loi de Newton (principe de l'inertie; seul le repos ou le MRU sont possibles). Les causes d'un mouvement circulaire sont différentes: dans ce cas, il doit exister une force, la force centripète, qui est dirigée vers l'axe de rotation. Ce modèle simplifié d'un manège met en évidence une telle force.
Si vous choisissez le second des quatre radio-boutons sur la partie supérieure droite, les vecteurs des forces exercées seront dessinés pour chacune des huit masses pendues: Le vecteur poids sera représenté en noir, la force de tension exercée par la corde en bleu. L'addition de ces vecteurs donne la force résultante (en rouge) et est identique à ce qu'on appelle la force centripète.
En plus de la simulation du manége (avec les vecteurs forces ou sans eux) le programme montre un croquis bidimensionnel simple des vecteurs forces et des valeurs numériques importantes du mouvement circulaire.
Si vous voulez observer exactement les vecteurs forces, vous pouvez arrêter la rotation en utilisant le bouton de "Pause / Reprise" ou le rendre dix fois plus lent avec l'option "Mouvement lent". Les champs de texte permettent de changer les valeurs des paramètres dans certaines limites (ne pas oublier de valider avec la touche "Enter"!).
Note: La simulation montre un mouvement circulaire avec une vitesse constante; les processus mettant les masses respectivement, en accélération ou en décélération, ne sont pas pris en compte. Les effets de la résistance d'air sont, aussi négligés.
Calcul de la vitesse d'un des sièges du manège.
 |
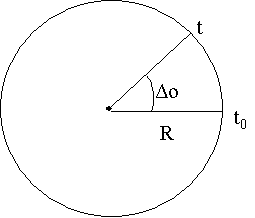Une vitesse, c'est une variation d'un espace parcouru sur
un temps. Soit  ,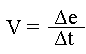
mais ici, l'espace parcouru est mesuré en radians ( )
et est dans un cercle. Pour connaître l'espace parcouru, il faut
multiplié l'angle  ,
par le rayon du cercle (R). Il en devient donc :  |
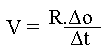Mais, ,
peut aussi s'écrire comme étant un cercle complet, soit 2Π (en radians)
et 
peut s'écrire T, (
T= la période, soit le temps qu'il faut pour faire un tour complet du cercle.).
Il en vient donc :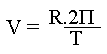 
,
la vitesse d'une chaise de ce manège se calcule donc par la formule : 
Vérifier les données numériques de l'animation ci-dessus. Pour ce
faire, cliquer sur valeurs numériques et effectuer le calcul grâce à la
formule. ( Période T = 4 s).
|
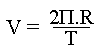
Cours en ligne ; physique.net : (c) Miseur Ludovic 2003
Animation : URL: http://home.a-city.de/walter.fendt/phf/carousel_f.htm
© Walter Fendt, 10 Mars 1999
© Traduction: Yves Weiss, 26 Janvier 2000
Dernière modification: 28 Janvier 2000
